
Enrique (Kiko) Galvez
At Colgate we strive to be teaching pioneers. We dare to step out of the box by rethinking content and inventing new teaching methods. In the sciences, faculty and students plunge into the depths of their disciplines armed with state-of-the-art technologies to ask new questions and explore an exciting scientific landscape never seen before.
BS, Pontifical Catholic University
PhD, University of Notre Dame
* = Student co-author
Article links to the file of the publication
"Electronics with Discrete Components" E.J. Galvez (Wiley, Hoboken, 2025).
This new edition incorporates the latest technological advances in the digital industry as they apply to making electronic circuits with individual integrated circuits. It adds many more exercises and problems plus labs that use Arduino and Teensy boards.

- "Quantum Inspired 3D Pendulum Beams" V. Rodriguez-Fajardo, T. Nguyen* and E.J. Galvez, Journal of Optics, 27, 045609 (2025).
We studied preparing optical beams in modes of the beam that mimicked the states of the quantum pendulum (Imagine a pendulum of atomic size). We prepared superpositions of modes (states) in such a way that the propagation represented time. Thus as we moved the camera along the beam we saw the quantum state changing. The image shown is of the beam in the "Fourier plane." It is a remarkable optical analog graph of the wavefunctions of the states involved in the superposition, where the angular position from the center is the angle of the pendulum and the distance from the center is the energy of the state. It is an analog energy-level diagram. The top and bottom halves of the image mirror each other. - “Young’s Double-Slit Interference Demonstration with Single Photons,” B. Luo,* L. Francis,* V. Rodriguez-Fajardo, F. Khoshnoud and E.J. Galvez, American Journal of Physics, 92, 308-316 (2024). Archive version.
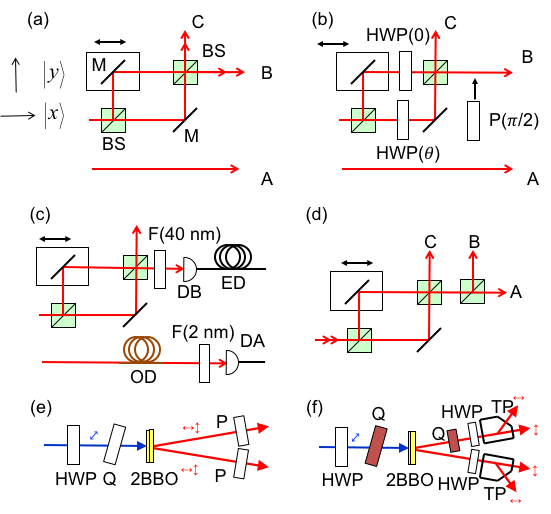
This work reports on a method to implement a demonstration of Young's double-slit experiment with single photons. It modifies the standard setup to do table-top experiments with correlated photons. In our work we resolved some of the challenges associated with this demonstration: spatial coherence and resolution. - “Nonlocal Mueller Polarimetry,” C.-J. You,* V. Rodriguez-Fajardo, L. Francis,* and E.J. Galvez, Proceedings of SPIE 12845, 1284509 (2024). We note that tables 1 and 3 contain typos. Will submit an erratum.
“Einstein Beams and the Diffractive Aspect of Gravitationally-lensed Light,” V. Rodriguez-Fajardo, T.P. Nguyen,* K.S. Hocek,* J.M. Freedman,* and E.J. Galvez, New Journal of Physics, 25, 0833033 (2023).
We developed a new form of laboratory astrophysics: simulating gravitational lensing. With it we were able to image the diffraction of gravitationally lensed light, as predicted by general relativity but never observed in astrophysical measurements. We also found a new type of optical beam that is a hybrid between non-diffracting beams and Gaussian beams, called Einstein beams.
“An easier-to-align Hong–Ou–Mandel interference demonstration,” N.S. DiBrita* and E.J. Galvez, American Journal of Physics 91, 307-315 (2023).
“Einstein beams carrying orbital angular momentum,” V. Rodríguez-Fajardo, T.P. Nguyen,* K.S. Hocek,* J.M. Freedman,* and E.J. Galvez, Proceedings of SPIE 12436, 124360C (2023). - “Direct measurement of the density matrix of a two-photon polarization qubit,” E.J. Galvez, A.D. Goldstein,* C.J. You,* V. Rodríguez-Fajardo, Li. Shi, and R.R. Alfano, Proceedings of SPIE 12373, 123730C (2023).
- “A curriculum of table-top quantum optics experiments to teach quantum physics,” E.J. Galvez, Journal of Physics: Conference Series 2448, 012006 (2023).
Quantum Optics Experiments To Teach Quantum Mechanics
Over the past 20+ years we have developed table-top experiments to teach the fundamentals of quantum mechanics: superposition,indistinguishability, entanglement. This article is a review of the experiments that we have designed and implemented.
- “Decoherence of photon entanglement by transmission through brain tissue with Alzheimer’s disease,” E. J. Galvez, B. Sharma,* F. K. Williams,* C.-J. You,* B. Khajavi, J. Castrillon, L. Shi, S. Mamani L.A. Sordillo, L. Zhang, and R. R. Alfano, Biomedical Optics Express 13, 6621-6630 (2022).
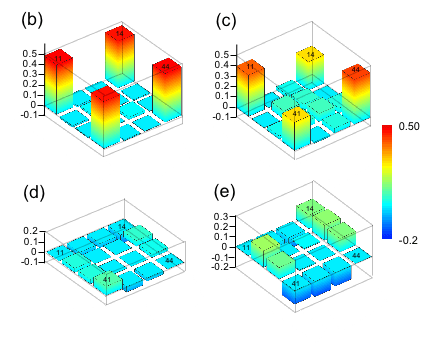
Quantum Decoherence as a Diagnosis Tool
Over the past seven years, we have been working on a technique that transmits entangled photons through tissue. We characterize the tissue by what it does to the entangled state of the photons. In this article, we found that entangled photons going through brain tissue with Alzheimer's disease experienced less decoherence than healthy samples. The figure shows the measured density matrix of the sample with the disease (left) and the healthy (right).
- “(2D+1) Pendulum Beams: Nin-diffracting Optical Spatial Wavepackets that Simulate Quantum Pendulum Dynamics,” T.P. Nguyen,* V. Rodriguez-Fajardo, and E.J. Galvez, Proceedings of SPIE 12017, 1201704 (2022).
- "Einstein Beams: Optical Beams Following Gravitationally Lensed Trajectories," E.J. Galvez and J.M. Freedman,* Proceedings of SPIE 11701, 117010U (2021).
- "Remote Quantum Optics Labs," E.J. Galvez, Proceedings of SPIE 11701, 1170106 (2021).
- “Pendulum Beams: Optical Modes that Simulate the Quantum Pendulum,” E.J. Galvez, F.J. Auccapuclla, Y. Qin,* K.L. Wittler,* and J.M. Freedman,* Journal of Optics 23, 024001 (2021).
Non-diffracting Pendulum Beams Reproduce the Quantum Pendulum
In this research, we create optical beams in a specific type of optical mode where the wave equation has the same form as the quantum equation for the single pendulum. As a consequence, the images that appear on a screen have an intensity proportional to the quantum probability.

“A Demonstration of Quantum Key Distribution with Entangled Photons for the Undergraduate Laboratory,” A. Bista,* B. Sharma,* and E.J. Galvez, American Journal of Physics 89, 111-120 (2021).
Demonstrating how Quantum Superposition can Uncover the Eavesdropper in Quantum Communications
In the quantum world, a measuring device gives outcomes of a measurement. To each outcome corresponds a state. So after a measurement, the system is left (or projected) in the state corresponding to the measured value. A quantum system can be in a superposition of states of the measuring device, so that a measurement modifies the state of the system. These quantum principles can be harnessed to detect an eavesdropper in a communication with photons. The measurement device detects the photon in one of 2 orthogonal states or possibilities. If the photons are sent in a superposition of these states and the eavesdropper makes a measurement, it would change the state of the photon so to reveal the action. We implement the generation and detection of the single photons using quantum entanglement, and simulate the eavesdropper with a dephasing optical element.
- “Transmission quantum state tomography of biological tissue,” E.J. Galvez, B. Sharma,* F.K. Williams,* B. Khajavi, and L. Shi, Asian Journal of Physics 29, 379-386 (2020).
- “Experiments with Correlated Photons” E.J. Galvez, in Experimental Physics: Principles and Practice for the Laboratory, W. Smith, Editor (Taylor & Francis, Boca Raton, 2020), pp 377-402.
- Poincaré-Bessel Beams: Structure and Propagation, B. M. Holmes* and E.J. Galvez, Journal of Optics 21, 104001 1-7 (2019).
- A Time-energy Delayed-choice Interference Experiment for the Uundergraduate Laboratory, J. Castrillon, E.J. Galvez, B. Rodriguez, and O. Calderon-Losada, European Journal of Physics 40, 055401 (2019).
- Quantum Optics Laboratories for Teaching Quantum Physics, E.J. Galvez, Proceedings of SPIE 11143, 111431A 1-6 (2019).
- Pendulum Beams: A Window into the Quantum Pendulum, E.J. Galvez, F.J. Auccapuclla, K.L. Wittler,* and Y. Qin,* Proceedings of SPIE 10935, 1093509 (2019).
Determining Vortex-Beam Superpositions by Shear Interferometry, B. Khajavi, J.R. Gonzales Ureta, and E.J. Galvez, Photonics 5, 5030016 (2018).
Determining Optical Vortices by their Wave-Ripples
Optical beams can carry optical vortices. These are wave tornados in the light. Should we combine two beams with vortices of distinct vorticicity, a striking phenomenon occurs. The resulting beam rearranges its vorticity so that it consists of a central vortex surrounded by an array of singly-charged vortices. The pattern of vortices reveals the vortex content of the original beams. We studied this phenomenon ten years ago, in work led by then Sean Baumann '08 (see story below Optics Express from 2009). In this work we use a "shear interferometer" to unravel this pattern in a simple and direct way. Behzad Khajavi, recent Ph.D. from Florida Atlantic University, did his dissertation research at Colgate and led the discovery of using shear interferometry to determine the vorticity of optical beams (Optics Letters 2017 below). Using this method, and with important contributions from Junior Gonzales Ureta, graduate student visitor from Peru, we developed a method to determine the vortex content of superpositions of vortex beams. These can be used to store information in optical beams. The figure below shows the wave ripples in the light beam, color coded to enhance the peaks and troughs of light waves (radians), featuring dislocations in the ripples caused by the vortices, and revealing that it was made by two beams with vorticity of +1 and -2.
Laser Imaging Polarimetry of Nacre, J.A. Jones, R.A. Metzler, A.J. D'Addario,* C. Burgess,* B. Regan,* S.Spano,* B.A. Cvarch,* and E.J. Galvez, Journal of Biophotonics (in press, March 28, 2018, DOI: 10.1002/jbio.201800026). Preprint.
Nacre Through Polarizing Glasses
In this work, we investigate the structure of nacre by passing polarized light through it. The way nacre scrambles the polarization of the light tells us about the type of shell that produced the nacre. It can be bivalve (such as pearl oyster), gastropod (such as abalone- figure) or cephalopod (such as nautilus). Six Colgate students participated in the research. B. Holmes has done more recent studies.
Multitwist Möbius strips and twisted ribbons in the polarization of paraxial light beams, E.J. Galvez, I. Dutta,* K. Beach,* J.J. Zeosky,* J.A. Jones, and B. Khajavi, Scientific Reports 7, 13653 1-9 (2017).
Möbius Twists in Light Fields
This publication reports on a stunning realization: light fields in generic conditions twist in 3 dimensions. We went to investigate on a simple situation: two optical beams crossing in free space. Our aim was to measure it the simplest way possible: with polarizers. It was not easy; it took us 5 years to solve this problem. In the article we report that knowing our particular geometry we can extract the 3-dimensional fields, and show that they indeed twist, forming either Möbius strips or twisted ribbons along a closed path in space. We show an example of experimentally extracted of the polarization orientation at the crossing of two beams- more details can be found in the article.
Monstar polarization singularities with elliptically-symmetric q-plates, B. Cvarch,* B. Khajavi, J.A. Jones, B. Piccirillo, L. Marrucci, and E.J. Galvez, Optics Express 25, 14937 (2017).
Generating Monstars using Liquid-Crystal Q-plates
Monstars are asymmetric topological dislocations. We have created them previously using superpositions of optical beams. A new type of engineered device invented by our colleagues at the University of Naples (B.P. and L.M.) known as the "q-plate" can use the birefringence of liquid crystals to impart dislocations onto optical beams. This has been shown by them previously with symmetric q-plates. As part of his summer (2016) and senior thesis research, Ben Cvarch '17 studied q-plates that were elliptically symmetric, and showed that they produce monstar disclinations of index zero (see images below). Behzad Khajavi continued Ben's work and measured monstars of index 1/2 with the same q-plates. Kudos to both. The article was selected as the "Editor's Pick" from the journal as an excellent research publication.
- Determining topological charge of an optical beam using a wedged optical flat, B. Khajavi and E.J. Galvez, Optics Letters 42, 1516-1519 (2017).
Determining the Orbital Angular Momentum of a Light Beam
In doing the previous work on monstars we stumbled onto a new method to determine the topological charge of a beam carrying orbital angular momentum. The orbital angular momentum per photon is the topological charge times Planck's constant over two-pi. In many instances it is important to know this parameter and we found a method to determine it visually using a minimum number of optical elements. All we need is a pair of lenses to make the wavefront planar, and a wedged optic. If the beam carries an optical vortex, and hence orbital angular momentum, then by reflecting it off a wedged optic we find a pattern of conjoined forks as shown in the figure. The topological charge is given by the number of tines minus 1.
- Monstar Disclinations in the Polarization of Singular Optical Beams, Enrique J. Galvez and Behzad Khajavi, Journal of the Optical Society of America A 34, 568-575 (2017).
Optical Monstars
This work is the culmination of a study of topological patterns that we can embed in the polarization of the light. In presents a study of all the monstars that can be produced with three modes of light. Monstars are disclinations or disruptions in a rotational order. Why do we care? They are present in many physical systems: crystal dislocations, magnetism, and topologies of surfaces and materials, to name a few. However, in most situations we cannot control the pattern that appears, or is very difficult to generate a pattern deliberately. Here we use light to explore all the possibilities. We have found many new patterns that have not been seen before. We find them surprisingly variable, often showing wild and crazy shapes. The experiments reproduce the theory very well. The figure below shows three types of monstars (predicted shapes are in first row, and measured ones are in the second row). They are characterized by their index: the number of turns that the lines (polarization) makes per turn around the center. Their indices are: +3/2 for the left pattern, 0 for the middle pattern, and -1/2 for the right pattern.
- Deducing 3-Dimensional Polarization Fields from Projective Measurements (Revised), Enrique J. Galvez and Ishir Dutta, Proceedings of SPIE 10120, 101200B (2017).
- Searching for the Helical-Gradient Force on Chiral Molecules Joshua A. Jones, Brian Regan,* Joshua Mills,* Behzad Khajavi, Jackson Painter* and Enrique J. Galvez, Proceedings of SPIE, 10120, 101200M (2017).
- Polarimetry of Pinctada Fucata Nacre Indicates Myostracal Layer Interrupts Nacre Structure, Rebecca A. Metzler, Joshua A. Jones, Anthony J. D'Addario* and Enrique J. Galvez, Royal Society Open Science 4, 160893 (2017).
Using Light's Polarization to Investigate Nacre
Nacre or Mother of Pearl is the colorful iridescent surface of shells. It has an amazing structure: a brick and mortar pattern of micron-sized crystals (bricks) embedded in organic matter (mortar). The crystals, made of aragonite, modify the polarization of the light as it passes through them. In this study we study the structure of nacre by examining what it does to the polarization of the light after it passes through a thin section, edge on. A stage of turbulence or disruption in the growth of the shell leaves a mark in the layers of nacre, similar to the way major geological events in Earth's history leave a mark in the geological layers of the soil. In our case the layer is known as the myostracal layer. In this work we were able to show a difference in the structure of nacre before and after this event using light. It is a unique experiment! The photo below shows imaging photos of the sample and a glimpse of our analysis. For more you must read the paper!
- Photon Entanglement Through Brain Tissue, Lingyan Shi, Enrique J. Galvez, and Robert R. Alfano, Scientific Reports 6, 3774 (2016).
Characterizing Brain Tissue with Entangled Photons
In this work we investigated how the entanglement in polarization between two photons of light survived when one photon passes through a thin slice of brain tissue. Before we did the experiment we thought that traveling through a messy medium of neurons and axons would wipe out the entanglement. What we found was surprising. The entanglement survived passage through tissue regardless of thickness! What mattered was not the thickness, but the amount of water and the type of tissue. Gray matter was quite transparent, but white matter was not. Other tissues, like kidney were not as transparent. The results that we present leaves us with one question: could we diagnose disease with this method? The question is still open. Stay tuned!
- Complex Light Beams, Enrique J. Galvez, Chapter article to appear in Deep Imaging in Tissue and Tissue-like Media with Linear and Nonlinear Optics, R. Alfano and L. Shi Eds. (Pan Stanford Publishing) forthcoming. Preprint
- The Poincare'-Sphere Approach to Polarization: Formalism and New Labs with Poincare' Beams, Joshua A. Jones, Anthony J. D'Addario,* Brett L. Rojec,* Giovanni Milione, and Enrique J. Galvez, American Journal of Physics 84, 822-835 (2016).
A New Approach and Lab for Teaching the States of Polarization of Light
In this article we propose incorporating the Poincare' sphere in introductory treatments of optics as a way to explain states of polarization. In particular, this approach makes an easy and intuitive connection between the polarization ellipse and its analytical description. We also present a new advanced laboratory where students explore all states of polarization in an interesting way: creating "holes" in laser beam and moving them within the beam. The holes are in reality the nulling of a certain state of polarization within a beam where the polarization varies across its transverse dimension. The figure below shows an example of the image of the beam with a particular state filtered out (left) and the extracted pattern after measuring it via polarimetry.
- High-Order Disclinations in Space-Variant Polarization, Behzad Khajavi and Enrique J. Galvez, Journal of Optics 18, 084003 (2016).
Exploring High-Order Disclinations in Polarization of Light Fields
In this work we investigated encoding topological features, known as disclinations, on the polarization of the light. Disclinations are dislocations of the rotational order of vectors, directions or lines. Think of your fingerprint. The skin ridges contort and at some points form patterns that are known as lemons and stars in topology, but loops and deltas in fingerprinting lingo. A next high-order pattern of a lemon is one where the lines are radial or form concentric circles (whorls in fingerprints). Since we deliberately encode these patterns in light, we can do so with both types in all orders, as shown in the figure. In this article we present the technique to generate these patterns. In the figure we show two data sets. False color encodes the orientation relative to the radial direction (radial is yellow; orthogonal is blue).
- High-Order Disclinations in the Polarization of Light, E.J. Galvez and B. Khajavi, Proceedings of SPIE 9764, 97640R (2016). Preprint
- Preparation of Poincare' beams with a same-path polarization/spatial-mode interferometer, Behzad Khajavi and Enrique J. Galvez, Optical Engineering 54, 111305 1-6 (2015).
Investigating Polarization Singularities with a more Efficient Interferometer
The work of the previous article uses a same-path interferometer using two spatial light modulators to study further polarization singularities that are not centered on the beam of light. The particular singularities that we study are called C-points, which are points where the orientation of the polarization ellipse is undefined, but around which the orientation rotates. This is seen in the figure below, where false color denotes ellipse orientation. The structure of the singularities has a triangular shape, where the vertices of the triangle and its center contain the C-points (lemon/monstars at the vertices and star at the center). Simulation is on the left and measurements are on the right. Small ellipses placed in random locations specify the state of polarization at that point.
- Physics from Planet Earth, J.C. Amato and E.J. Galvez (Taylor and Francis, 2015). New general physics textbook that offers a fresh new approach to teaching calculus-level mechanics.
- "Light Beams with Spatially-Variable Polarization," E.J. Galvez, in Handbook of Fundamentals of Photonics and Physics, D.L. Andrews, Editor (Wiley-Wise, 2015)
- "Space-Variant Polarization Patterns of Non-Collinear Poincare Superpositions," E.J. Galvez, K. Beach,* J.J. Zeosky, and B. Khajavi, Proceedings of SPIE 9379, 93790A 1-8 (2015).
"Encoding and Decoding Non-separable States of Polarization and Spatial Mode of Single Photons," B. Khajavi, X. Cheng,* K. Kebede,* and E.J. Galvez, Proceedings of SPIE 9379, 93790G 1-8 (2015) - "Resource Letter SPE-1: Single-Photon Experiments in the Undergraduate Laboratory," E.J. Galvez, American Journal of Physics 82, 1018-1028 (2014). Journal
Quantum Optics Laboratories to Teach Quantum Physics
The previously listed article is a review of experiments with single photons adapted to teach quantum physics. It also lists the original articles that inspired those demonstrations, along with useful information for those interested in doing their own implementations.
- “Polarimetry of Nacre in iridescent shells,” R.A. Metzler, C. Burgess,* B. Regan,* S. Spano,* and E.J. Galvez, Proceedings of SPIE, 9187, 918704 1-11 (2014).
- “Imaging single photons in non-separable states of polarization and spatial mode,” X. Cheng* and E.J. Galvez, Proc. SPIE 9225, 922506 1-9 (2014).
- "C-Point singularities in Poincare beams," E.J. Galvez, B.L. Rojec, K. Beach, and X. Cheng, in Coherence and Quantum Optics X, Editors N.P. Bigelow, J. Eberly and C.R. Stroud (Optical Society of America, 2014), pp. 71-77.
- "Mapping of all polarization-singularity C-point morphologies," E.J. Galvez, B.L. Rojec,* and K. Beach, Proceedings of SPIE 8999, 89990I 1-8 (2014). Journal
- "Generation of isolated asymmetric umbilics in light's polarization," E.J. Galvez, B.L. Rojec,* V. Kumar, and N.K. Viswanathan, Physical Review A - Rapid Communications 89, 013801 1-4 (2014); e-preprint: arXiv:1402.5442v1).
Fingerprints of Optical Fields
Human fingerprints contain patterns of ridges or lines that converge in loops or stars known as line singularities. Nature also contains “fingerprints,” patterns of line singularities that describe flow and geometry, mathematically revealing topology and representing indefinite quantities. Through our work (previous citation) we use beams of light to encode those line singularities, which are classified into three types: lemons (loops), stars, and monstars (a third, intermediate, kind). Each type represents the level of asymmetry and the handedness of the lines twirling or converging in the singularity. We encode line singularities onto light not through images but through their polarization properties — the direction, magnitude and phase of the electric and magnetic fields’ oscillations, which could be linear, circular, or elliptical. The beams of light we produce have field vectors describing ellipses that vary from point to point in their cross-section, with the ellipse axes forming the line patterns. While pursuing this encoding process, we were able to create beams of light that contain any desired pattern of lines, symmetric or asymmetric, including monstars, the type of singularity pattern that, up to now, has been elusive. By maintaining such exquisite control over the parameters of the light beam, this new type of optical fingerprint can lead to innovative ways to encode and recognize information. Picture Legend (below): Line singularity pattern (left) of a monstar and its recreation in a light beam (right) via the orientation of the polarization ellipses of the light field. False color encodes orientations.
- "Imaging optical singularities; Understanding the duality of C-points and optical vortices," E.J. Galvez, B.L. Rojec,* and K.R. McCullough,* Proceedings of SPIE 8637, 863706 1-10 (2013).
- "Poincare-beam patterns produced by non-separable superpositions of Laguerre-Gauss and polarization modes of light," E.J. Galvez, S. Khadka,* W.H. Schubert,* and S. Nomoto* Applied Optics 51, 2925-2934 (2012).
Introducing Poincare' Beams
It is now straight forward to produce optical beams in helical modes. In the article in Optics Express we superposed two beams with different helical modes, but same polarization. If we superpose two optical beams with different helical modes and with opposite (orthogonal) states of polarization, we get a new type of beams known as Poincare' beams. The mode of the resulting beam is also known as a Poincare' mode, because it carries single or multiple mappings of the states on the Poincare' sphere onto the transverse mode of the beam. Thus, these beams have a state of polarization that varies from point to point. An optical beam may have all states of polarization in its transverse profile. The figure below shows the polarization map created by a particular superposition. The center is right-handed circular. As we move away from the center the polarization becomes elliptical, then linear, and continuing into elliptical with the opposite handedness, reaching circular again, and so on. The orientation of the ellipses also varies for different orientations.
- Electronics with Discrete Components, E.J. Galvez (Wiley, Hoboken, 2012)
A new electronics textbook that covers digital and analog electronics. It focuses on the most important electronic devices, their fundamentals and their use in simple circuits. The text includes inexpensive laboratory exercises that follow the discussions. The book takes an innovative approach by covering digital before analog. - "Poincare Modes of Light," E.J. Galvez and S. Khadka,* Proceedings of SPIE8274, (2012).
- "Proposal to produce two and four qubits with spatial modes of two photons," E.J. Galvez, Proceedings of SPIE 8274 (2012).
- "Vector Beams in Free Space" E.J. Galvez in Angular Momentum of Light, D.L. Andrews and M. Babiker Eds. (Cambridge University Press, Cambridge, 2012).
- "Preparing photon pairs entangled in any desired spatial modes via interference" E.J. Galvez, Proceedings of SPIE 8057, 805706 (2011).
- "Interferometric measurement of the helical mode of a single photon", E.J. Galvez, L.E. Coyle,* E. Johnson,* and B.J. Reschovsky,* New Journal of Physics 13, 053017 1-10 (2011).
Measuring the Helical Mode of Single Photons
Light beams can be prepared in helical modes, where the wavefront has corkscrew shape. The slanted wavefronts of the beam give it angular momentum. Such a beam has a clear picture as a classical wave, but what about the photons that make up this beam? Quantum mechanics predicts that each photon carries the entire mode, as a wave of probability. In this work we set out to confirm via interference measurements that each photon can carry a helical mode. Picture legend (below): On the left side is a sketch of the helical wavefront, as understood in terms of waves whose phase advances about the axis of the beam. On the right is a measurement of the mode of single photons taken one photon at a time by scanning a single-pixel camera in a transverse plane.
- Modern Introductory Physics, C.H. Holbrow, J.N. Lloyd, J.C. Amato, E.J. Galvez and M.E. Parks (Springer-Verlag, New York, 2010).
- The second edition of a text for a first physics course on modern physics geared for first-semester students. It covers all the main topics of modern physics building up to a coverage of quantum physics at the introductory level. That is, all the subjects are presented at the algebra-trig mathematical level. Topics include how do we know that atoms, electrons and photons exist; the wave-particle duality of objects, relativity and its consequences, energy levels of atoms, quantum interference and entanglement. The idea is to teach the exciting topics in physics from the very beginning.
- "Qubit Quantum Mechanics with Correlated-photon Experiments," E.J. Galvez, American Journal of Physics78, 510 (2010).
Measuring Violations of Bell Inequalities in the Undergraduate Lab- with a Laser Pointer
We developed a series of experiments for undergraduates that test fundamentals of quantum mechanics (See Am. J. Phys. article below). Technological advances allowed the apparatus for these labs to fit in a breadboard (photo below), and use inexpensive options, such as a blue laser pointer for the source of light. We have created a laboratory component of a course on quantum mechanics, where students make fundamental tests on the existence of photons, quantum interference-that each photon interferes with itself, and local realism-that objects (and photons) do not have an inherent reality and could be correlated instantaneously with other events at distant locations. The latter includes measurement of a violation of Bell inequalities-all in an afternoon lab. The photo shows one setup, with a laser pointer in the foreground generating blue photons (following dashed lines). Photons hit a crystal that produces pairs of red photons (must conserve energy) entangled in their polarization properties. Downstream, a meter away, optics and photon detectors measure the correlations between photons to show that nature does not follow local realism. (See also link to dedicated web page above.)
- "Imaging Spatial-Helical Mode Interference of Single Photons," E.J. Galvez, E. Johnson,* B.J. Reschovsky,* L.E. Coyle,* and A. Shah,* Proceedings of SPIE 7613 (2010).
- "Correlated-Photon Experiments for Undergraduate Labs," E.J. Galvez (Unpublished 2010). This is a detailed description of experiments for doing quantum mechanics labs.
- "Gaussian Beams," E.J. Galvez (unpublished-2014 update). This is a set of notes that I put together to complement a course in optics. It includes Gaussian beams, high order modes, and orbital angular momentum.
- “Propagation dynamics of optical vortices due to Gouy phase,” S.M. Baumann,* D.M. Kalb,* L.H. MacMillan,* and E.J. Galvez, Optics Express 17, 9818-9827 (2009).
Rotating Vortices
In the work of the previous citation we report on research that investigated the superposition of optical beams carrying an optical vortex. It follows a previous report (SPIE 2006). Optical vortices are specified by the topological charge, or the number of times that the phase winds by 360 degrees per turn around the beam. The resulting beam splits into a symmetric array of singly charged vortices, which rotate about the beam axis as the beam propagates. Photo Caption (below): Interferogram of an optical beam carrying 7 optical vortices. The optical vortices appear in the interferogram where one sees forks in the pattern. In the figure there is one in the center and 6 in the periphery; the interference of beams with topological charge +1 and -5.
- “Composite Vortices of displaced Laguerre-Gauss beams,” D.M. Kalb* and E.J. Galvez, Proceedings of SPIE 7227, 72270D 1-8 (2009).
- "Bell-Inequality Violations with Single Photons Entangled in Momentum and Polarization," B.R. Gadway,* E.J. Galvez, and F. De Zela, Journal of Physics B 42, 015503 1-9 (2009).
Self-entangled Photons
The defining state in the era of quantum information is entanglement. Entanglement of two particles embodies a striking but glamorous feature of quantum physics: nonlocality. An entangled state is a nonseparable state of two particles; a state that cannot be expressed as the state one particle independent of the other. Entanglement is also a requisite ingredient for measuring a violation of Bell's inequalities. A single particle can be put in a superposition of two modes, or degrees of freedom, such as polarization and direction of propagation, something that is easily done by a polarizing interferometer. Would single photons in such a superposition violate Bell's inequalities? That is what the work cited by the previous article set out to do. The answer that we found is "yes." One does not need entanglement of two particles to violate Bell's inequalities. This measurement falsifies realism but not nonlocality.
- “Singular Optics and Phase Properties,” E.J. Galvez in Structured Light and Its Applications, D.L. Andrews Ed. (Academic Press – Elsevier, 2008), pp 63-77.
- "Composite vortex patterns formed by component light beams with non-integral topological charge," E.J. Galvez and S.M. Baumann,* Proceedings of SPIE 6905, 69050D (2008).
- "Orbital Angular Momentum of Light in Optics Instruction," E.J. Galvez and N. Zhelev.* ETOP conference proceedings (2007).
- "Quantum Optics Experiments with Single Photons for Undergraduate Laboratories," E.J. Galvez and M. Beck. ETOP conference proceedings (2007).
- "Phase Shifting of an Interferometer using Nonlocal Quantum-State Correlations," E.J. Galvez, M. Malik,* and B.C. Melius,* Physical Review A-Rapid Communications 75, 020302(R) (2007).
Spooky Phase Shifting
In this article (previous citation) we describe an experiment with photon pairs that exemplifies the striking predictions of quantum mechanics. One photon goes through an interferometer but its entangled partner does not. We record the coincidences of the photon and its partner, and see interference. Strikingly, since both share the same state, we shift the phase of the interference pattern by manipulations on the photon that does not go through the interferometer. These manipulations on the other photon involve shifting the phase between its polarization states, a phase that is known as Pancharatnam-Berry geometric phase.
- "Non-integral Vortex Structures in Diffracted Light Beams," S. Baumann* and E.J. Galvez, Proceedings of SPIE 6483, 64830T (2007).
- "Gaussian Beams in the Optics Course," E.J. Galvez, American Journal of Physics, 74, 355-361 (2006).
- "Composite Optical Vortices Formed by Collinear Laguerre-Gauss Beams," E.J. Galvez, N. Smiley,* and N. Fernandes,* Proceedings of SPIE 6131, 19-26 (2006).
- "Nonlocal Labeling of Paths in a Single-Photon Interferometer," M.J. Pysher,* E.J. Galvez, K. Misra,* K.R. Wilson,* B.C. Melius,* and M. Malik* Physical Review A 72, 052327 (2005).
A Spooky Quantum Eraser
The article in the previous citation describes an experiment with photon pairs that were entangled in polarization. The actions on one photon affect the state of both- alas Einstein's famous incredulous phrase "spooky action at a distance." One photon went through an interferometer, but the apparatus detected both photons. Quantum mechanics states that there is quantum interference when the paths that interfere (those of the interferometer in this case) are indistinguishable. If the path information is available, then there is no interference. One can change the distinguishability of the path information through actions that can occur after the light goes through the interferometer. This delayed-choice action is known as the quantum eraser. In our work we make the paths distinguishable or not, including erasing the path information, by actions on the photon that does not go through the interferometer. The actions on this photon affect the state of both, and so affects whether we see interference or not. Quoting Neils Bohr: "Anyone who is not shocked by quantum mechanics has not fully understood it."
- “Interference with correlated photons: Five quantum mechanics experiments for undergraduates,” E. J. Galvez, C. H. Holbrow, M. J. Pysher,* J. W. Martin,* N. Courtemanche,* L. Heilig,* and J. Spencer,*” American Journal of Physics 73, 127-140 (2005).
Photons to Learn Quantum Physics
At the heart of quantum mechanics is quantum superposition: A physical system can be two mutually exclusive possibilities as long as it is indistinguishable to us which possibility it is. This article reports on our efforts to teach this through a series of experiments with single photons going through a device that puts them in a state of superposition (an interferometer); a superposition of traveling distinct paths. We manipulate the information about which path the photon takes after it has passed the interferometer- a recreation of the quantum eraser. Interference appears or disappears depending on whether the path information is available or not. As time has gone by, the experiments have become increasingly simple and affordable. We have created a quantum eraser lab experience for our first-year modern introductory physics course. The figure below shows an example of the data that students get. In the first section the paths of the interferometer are indistinguishable and so we see interference (oscillations-a sign of superposition). When the path information is made available (via polarization-labeling of the paths) the interference disappears (middle section). This distinguishable information can be erased after the photons pass through the interferometer by placing a polarizer in their path before they reach the detector. As a consequence, the oscillations reappear (last section).
- “Existence and Absence of Geometric Phases Due to Mode Transformations of High-Order Modes,” E. J. Galvez and M. O’Connell,* Proceedings of SPIE 5736, 166-172 (2005).
- “Axial Control of Irregularly Shaped Microscopic Objects with Light Beams in High-Order Cartesian Modes,” E.J. Galvez, A. Weiss, G. Newbury, P.J. Crawford, and H.I. Sztul, Proceedings SPIE 5514, 674-677 (2004).
- “Undergraduate Laboratories Using Correlated Photons: Experiments on the Fundamentals of Quantum Physics,” E.J.Galvez, in Invention and Impact: Building Excellence in Undergraduate Science, Technology, Engineering and Mathematics (STEM) Education, (AAAS, 2004) pp 113-118.
- Observation of New Modal Patterns in Experiments with Hermite-Gaussian and Laguerre-Gaussian Laser Modes, K. Contreras, G. Baldwin, F. DeZela and E.J. Galvez, Proceedings SPIE 5522, 336-341 (2004).
- “Measurements of the Geometric Phase of First-Order Optical Gaussian Beams,” E.J. Galvez, H.I. Sztul,* and P.J. Haglin,* Coherence and Quantum Optics VIII (Edited by N. Bigelow et. al., Kluwer Academic/PlenumPublishers, 2003), 387-388.
- “Geometric Phase Associated with Mode Transformation of Optical Beams Bearing Orbital Angular Momentum,” E.J. Galvez, P.R. Crawford,* H.I. Sztul,* M.J. Pysher,* P.J. Haglin,* and R.E. Williams, Physical Review Letters 90, 2039011-4 (2003).
A New Optical Geometric Phase
In the previous article we present the first demonstration of a geometric phase obtained by varying the transverse mode of an optical beam. If we map all the possible modes onto the surface of a sphere, starting with one mode, changing it to another, and then to another, and then returning to the initial state, results in the introduction of a phase onto the light beam. The interesting part is that the phase depends on the sequence of steps in the transformation--the topology of the path followed in mode space. This is similar to translating a pencil on the surface of a ball, following a path, and returning to the starting point. If the path encloses any area, at the end the pencil will be pointing in a direction that is different than the starting point. This is a geometric phase. In our experiment, we traveled this path on the ball of modes, and measured the phase. The image in the cover photo of the journal shows two modes (top left) that are set to interfere. If we superpose them they generate an asymmetric pattern. If we change the phase by conventional means we see the rotation of images (top right), which is well known. When we introduce a geometric phase, we also see rotated images (bottom row).
- “Photon Quantum Mechanics and Beam Splitters,” C.H. Holbrow, E.J. Galvez, and M.E. Parks, American Journal of Physics 70, 260-265 (2002).
- “Applications of Geometric Phase in Optics,” E.J. Galvez, Recent Research Developments in Optics 2, 165-182 (2002).
- “Achromatic Polarization-Preserving Beam Displacer,” E.J. Galvez, Optics Letters 26, 971-973 (2001). PDF
- “Appearing and Disappearing Strong-Field (2d+time) Resonances in H Atoms,” E.J. Galvez, P.M. Koch, D. Richards, S.A. Zelazny, Physical Review A 61, 060101-4 (2000).
- “Variable Geometric Phase Polarization Rotators for the Visible,” E.J. Galvez, M.R. Cheyne,* J.B. Stewart,* C.D. Holmes,* H.I. Sztul,* Optics Communications 171, 7-13 (1999).
Inventing Optical Rotators
The polarization of the light can be rotated by sending the light through an off-plane trajectory. This can be accomplished with a series of mirrors but only if these act as ideal mirrors. Real mirrors in principle introduce reflection phases that change the state of polarization, and this also depends on the wavelength of the light. In the article above we present a study of this effect and propose an achromatic optical rotator, the "variable compensating phase shift (VCPS) rotator" that is immune to reflection phases, and shown in the image below.
- “Geometric Phase of Optical Rotators,” E.J. Galvez and C.D. Holmes,* Journal of the Optical Society of America A 16, 1981-1985 (1999).
Geometric Phase Rotators
The image that light carries is rotated if the light is reflected by a sequence of mirrors to describe an off-plane trajectory. This rotation is adjudicated to a topological phase, known as geometric phase. What is interesting is that the amount of rotation can be computed in terms of the topology of the trajectory of the light. It is related to the parallel transport of a vector on a curved surface. The previous article describes popular optical systems in terms of this concept. It generalizes the operation of the pair of Porro prisms, contained in every pair of binoculars to complement the lenses of the device. In such a system the lenses invert the image, and the pair of Porro prisms, oriented perpendicular to each other, invert the image back to be upright to the observer. If the Porro prisms are not oriented perpendicular to each other, the image rotated by an amount related by the relative angle formed by the two prisms, as shown in the figure below. This rotation is due to the topology of the path of the light, and is computed using the geometric construction explained in the article.
- “Beyond (1D+time) Dynamics in the Microwave Ionization of Excited H Atoms: Surprises from Experiments with Collinear Static and Linearly Polarized Electric Fields,” P.M. Koch, E.J. Galvez, S.A. Zelazny, Physica D, 131, 90-109 (1999).
- “Use of Four Mirrors to Rotate Linear Polarization but Preserve Input-Output Collinearity. II” E.J. Galvez and P.M. Koch, Journal of the Optical Society of America A 14, 3410-3414 (1997).
- “Blackbody-Induced Resonances Between Rydberg Stark States of Na.” E.J. Galvez, C.W. MacGregor,* B. Chaudhuri,* S. Gupta, E. Massoni, and F. De Zela, Physical Review A 55, 3002-3006 (1997).
- Studies of complex light and optical singularities
- Quantum interference with single photons
- Development of teaching laboratories for undergraduates
- Experimental atomic physics with atoms in highly excited (Rydberg) states.
Professor Galvez is an atomic and optical physics experimentalist. Recently his studies have focused on optics and quantum optics. These include fundamental studies of the geometric phase in optics, optical beams in high-order modes, singular optics, photon entanglement and studies of quantum interference with correlated photons. Prof. Galvez is also interested in physics education and in the development of new physics laboratories for undergraduates.
- Fellow of the International Society for Optics and Photonics (SPIE), 2024.
- Fellow of the American Physical Society, 2024.
- Recipient of the 2020 Jonathan F. Reichert and Barbara Wolff-Reichert Award for Excellence in Advanced Laboratory Instruction from the American Physical Society.
- Fellow of the Optical Society of America, 2018.
- 2010 Award to Faculty Member for Research at an Undergraduate Institution, from the American Physical Society.
- External grants: Research Corporation, 1990, 2000 and 2006, National Science Foundation – physics research, 1992, 2000, 2009, 2015, 2018; National Science Foundation-education, 1994, 2000, and 2005; Air Force Research 2009, 2010
- Picker Interdisciplinary Institute Grant 2013-2015, 2017-2019.
- Mentored students who received (Bryce Gadway, 2008) or were finalists (Matt Pysher, 2006) of the Apker Award of the American Physical Society for best research by an undergraduate.